- QUELQUES NOTIONS DE SON :
PROPAGATION, MESURES, NUMERISATION...
Définition :
- Le son est une onde produite par une vibration mécanique (la membrane d'un haut-parleur par exemple). On associe souvent l'image d'une pierre tombant dans l'eau et faisant des petites vagues tout autour du point d'impact. La comparaison est tout à fait valable quant au fait que ce sont les vagues (ou les ondes) qui se déplacent et non la matière elle-même.
La vague se déplace, mais pas l'eau, et de la même façon, un son ne déplace pas l'air (le son ce n'est pas du vent !).
Ce qui explique d'ailleurs plusieurs choses :
- il n'y a pas de son dans l'espace : il n'y a rien pour transporter l'onde.
- le son ne se propage pas à la même vitesse selon la densité, la matière, la température... :- 344 m/s (mètres par seconde) dans l'air à 20 °C
1482 m/s dans l'eau
- 344 m/s (mètres par seconde) dans l'air à 20 °C
- La fréquence d'un son se mesure en Hertz / Hz (ce sont des cycles par seconde) et détermine la hauteur (entre autres) de ce son (ou la note).
Plus un son est bas (une guitare basse, une ambiance à la Lynch...), plus il aura une fréquence faible.
L'Homme peut "théoriquement" percevoir des sons entre 20Hz et 20 000Hz (ou 20kHz), sachant qu'en moyenne, on perd 1000Hz par tranche de 10 ans, et donc une personne de 40 ans n'entend plus que jusqu'à 16 000Hz !
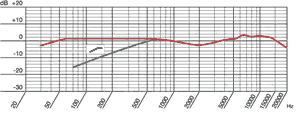
Pour un micro dédié à l'enregistrement sonore de fiction par exemple, il vaut mieux essayer d'en trouver un (ou deux) dont la bande passante se rapproche le plus de celle de notre oreille, mais un tel micro est encore rare et cher. Même si certains captent les mêmes fréquences, il y a toujours des pics et/ou des trous à certaines fréquences, donnant ainsi forcément une "couleur" au micro.
Sur cet exemple, on voit bien que le micro a une faiblesse autour des 2000 Hz :
Numérisation du son ou comment transforme t'on un son en binaire ?
- Graver un CD revient a lui faire des petits trous qui représentent des 0 et des 1 :
- Photo d'un CD en gros plan :

Exemple : sur un disque vinyl, si on regarde le sillon de trés près, on peut apercevoir de chaque côté la "wave" correspondante au canal gauche et droit, c'est à dire la forme exacte qu'a le son dans l'air.
2. L'oreille humaine percevant les sons entre 20 et 20 000 Hz, et selon le théorème de Nyquist :- La fréquence d'échantillonnage (sampling) doit être égale ou supérieure au double de la fréquence maximale contenue dans le signal.
Concrètement, échantillonner un son à une fréquence de 44 100 Hz signifie que l'on va mesurer 44 100 fois par seconde la hauteur de la courbe.
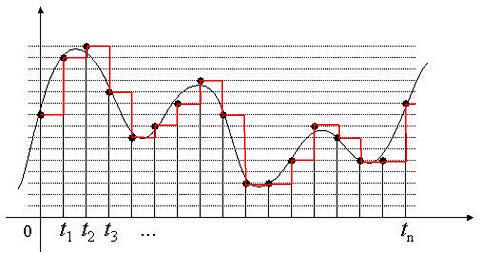
Sur cette courbe, si on échantillonne en qualité CD à 44 100Hz, on ira de t1 à t44100 pour une seconde.
L'avantage d'échantillonner un son à une fréquence plus élevée (48 000 Hz par exemple) peut être pour le traitement sonore par exemple (effets, shifting...), qui fera alors perdre moins de qualité.
3. Ensuite, vient la notion de quantification (quantization), qui est en fait la mesure de la hauteur de la courbe du son, qui dépend du nombre de bits alloué. Par exemple, pour le CD, la quantisation se fait avec 16 bits, ce qui offre 2^16 (ça fait 65536 pour ceux qui comptent lentement) valeurs possibles, qui seront donc du type : 0010011101001100 (avec 16 digits qui sont soit 0 soit 1).
Il y a donc un perte évidente de la qualité, mais "théoriquement", grâce au théorème précédemment cité, cette perte est inaudible (ce qui s'est avéré faux tout compte fait, d'où les nouveaux formats qui sont déjà apparus, comme le DVD-Audio ou le SACD par exemple).
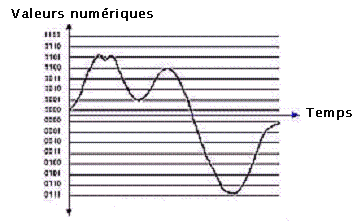
Le son analogique de la figure précédente est numérisé selon la "courbe" rouge. On aperçoit aisément le fait que cela n'est pas parfait, même si en mesurant 44 100 fois par seconde, la différence est infime.
Exemple : La courbe ci-dessous représente un échantillonage à 4 bits, soit 16 valeurs possibles, ce qui n'est pas envisageable bien sûr, tant la qualité serait faible :
- Taux d'échantillonnage x Nombre de bits x Nombre de secondes x Nombre de voies
Exemple pour une minute de son stéréo en qualité CD :
44100 x 16 x 60 x 2 = 84 672 000 bits soit 10 584 000 octets soit environ 10 Mo. - Photo d'un CD en gros plan :
SOURCES :